
Олимпиадные задания по физике 11 класс
Олимпиадные задания по физике для 11 класса
Неподвижное атомное ядро распадается на два осколка массой m1 и m2. Определить скорости осколков, если при распаде ядра выделяется энергия E.
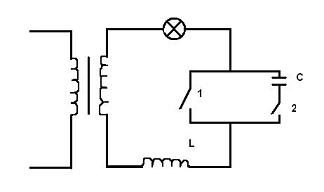
Задача 2 :
Почему при замыкании ключа 1 лампочка, включенная в цепь, как показано на рисунке, горит слабее, чем при замыкании ключа 2.
Задача 3 :
Два груза общей массой m = 1 кг, соединённые пружиной жёсткостью 100 Н/м, висят на нити. Найти все возможные расстояния, на которые можно оттянуть вертикально вниз и затем отпустить нижний груз, чтобы при последующих его колебаниях верхний груз оставался неподвижным.
Задача 4 :
В колбе находится вода при 0С. Выкачивая из колбы воздух, замораживают воду посредством её испарения. Какая часть воды при этом испарилась, если притока тепла нет? Удельная теплота испарения воды r = 2.26*10^6 Дж/кг, удельная теплота плавления льда равна 3.3*10^5 Дж/кг.
Задача 5 :
Плитка, включенная в сеть батареи, выделяет мощность 1000 Вт. Две таких плитки, включенных параллельно, выделяют мощность 1900 Вт. Какую мощность будут развивать три параллельно подключенные к этой батарее такие же плитки?
Задача 6 :
Определить показатель преломления n жидкости.
Оборудование.
Прозрачный цилиндрический сосуд с небольшим отверстием в боковой стенке (сверху сосуд открыт, а стенки сосуда заклеены темной бумагой, кроме вертикальной щели, расположенной диаметрально к отверстию), непрозрачная кювета с неизвестной жидкостью, полупроводниковый лазер (лазерная указка), штатив, линейка, миллиметровка, липкая лента, карандаш, прищепка.
Решение :
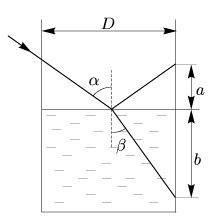
Наливаем воду почти до самого отверстия и пускаем через него луч лазера.
Происходит разделение луча на отраженный и преломленный (рис.).
Измеряем AC = a и BC = b.
Поскольку уровень воды близок к отверстию, то OC ≈ D.
Из закона преломления sin α = n sin β и измерений ctg α = a / D, ctg β = b / D
находим b2 = n2a2 + (n2 – l) D2.
Изменяя угол падения луча, снимем зависимость b от a.
Тогда по углу наклона графика b2 (a2) найдем n2, а, следовательно, и сам показатель преломления n.
Задача 7 :
Брат и сестра по очереди из одного пакета берут конфеты: брат — одну конфету, а сестра — две, брат — три конфеты, а сестра — четыре, брат — пять, сестра — шесть и т.д.
Когда конфет в пакете осталось меньше, чем должен взять тот, чья очередь наступила, он забрал все оставшиеся.
Сколько конфет было в пакете, если у брата в итоге оказалась 101 конфета?
Задача 8 :
Восемь различных цифр от 1 до 8 расставлены в вершинах куба.
На каждом ребре записан модуль разности цифр, находящихся в вершинах этого ребра.
Может ли сумма всех 12 чисел на ребрах быть равной
а) 40
б) 41
Задача 9 :
Про функцию f(x) известно, что при любых a и b выполняется равенство:
f(a + b) + f(a - b) = 2f(a)f(b).
а) Верно ли, что f(x) — четная функция?
б) Приведите пример непостоянной функции f(x), удов-летворяющей условию задачи.
Задача 10 :
Любую вершину треугольника можно сдвигать по проходящей через нее прямой, параллельной противоположной стороне.
Можно ли такими операциями превратить равносторонний треугольник со стороной 1 в прямоугольный треугольник с катетами, равными 1
Задача 11 :
Докажите, что для любых положительных чисел a, b и c справедливо неравенство
a3b + b3c + c3a > a2bc + b2ca + c2ab.
Задача 12 :
В неравнобедренном треугольнике ABC проведена медиана AD, ∠DAC + ∠ABC = 90o.
Найдите угол ∠BAC.
Вар-т 1 Вар-т 2 Вар-т 3 Задания с ответами